Exploring the identity a²-b² = (a-b)(a+b)

Introduction

There are many possible approaches to understanding this identity. Recently Peter Hendrickson asked me who my target audience is, and I told him it was me, assuming that for some reason I was ignorant about the item under discussion. For this identity, I would be sure to tell myself that there are various algebraic rewritings of the identity. There are three broad classifications:

• An identity that rewrites a difference of squares as a product, and its special cases:
  • a²-b² = (a-b)(a+b)
  • 1-x² = (1-x)(1+x)
  • x²-1 = (x-1)(x+1)
  • (x)²-(x-1)² = 2x-1
• An identity that rewrites a product as a difference of squares, and its special cases:
  • uv = ((u+v)/2)² - ((u-v)/2)²
  • u = ((u+1)/2)² - ((u-1)/2)²
  • 1 = ((w+1/w)/2)² - ((w-1/w)/2)²
• "Others", such as
  • a-b = (a²-b²)/(a+b)
  • a+b = (a²-b²)/(a-b)
  • ((x+h)²-x²)/h = 2x+h
  • C = (√(x+C)-√x)(√(x+C)+√x)

Throughout the discussion I would tell myself that the above identities hold in more general settings: the elements don't need to be real numbers, and the operations don't need to be multiplication and addition of reals. Also, with any algebraic result, I always want to know about geometric interpretations or consequences, so I'd be sure to mention something about that. Ditto for any physical interpretation. And, I'd mention something about generalizations and related identies: e.g. What about the difference of cubes, what about the product of three elements, what about the sum of squares, etc.

Okay, that's the broad overview and plan of attack. Now let's dig in.

Rectangles and Squares

The square of a positive real s, as in "s raised to the power 2", i.e. s², is the area of a square with side length s. The product of two positive reals a and b is the area of a rectangle with sides of length a and b.

Using these geometric interpretations, it's clear that the identity is saying something about areas of squares and rectangles.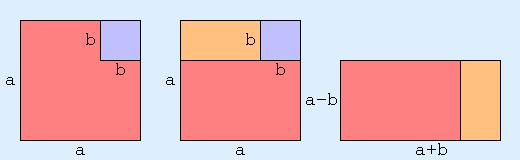

The above diagram gives some insight, via geometric dissection, about why the identity is true.

At this point, I'd like to make a little digression into symmetry considerations. In the above geometric sequence, an arbitrary choice was made, and the initial symmetry of the picture was broken. We could just as easily have gone the other way: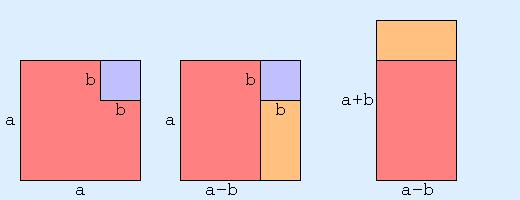

Strangely enough, this actually leads to a result. Considering both diagrams together, and forming a "superposition", we should expect that a²-b² is some kind of weighted average of (a-b)(a+b) and (a+b)(a-b). Since the two items are the same, this doesn't produce anything new. But, what if they weren't the same? What if multiplication were not commutative (i.e. xy was not the same as yx). This would be the case if a and b were n by n square matrices, or if they were quaternions. In that case, the identity would not be true. Using quaternions for example: i²-j² is 0, but (i-j)(i+j) is not.

Going back to algebra, this is because (a-b)(a+b) = a²+ab-ba-b², and ab and ba don't cancel each other out to give a final result of a²-b², unless ab=ba.

But, combining the two versions:
(a-b)(a+b) = a²+ab-ba-b²
(a+b)(a-b) = a²+ba-ab-b²
we do get that
(a-b)(a+b) + (a+b)(a-b) = 2(a²-b²).

Assuming it makes sense to divide by two, we get a weighted average identity
a²-b² = (1/2)(a-b)(a+b)+(1/2)(a+b)(a-b)
which is still true even when multiplication is not commutative.

I must admit at this stage that I don't know of any use for this, but I couldn't resist mentioning it.

Money

After that digression into abstract generality, it's time to go back to the concrete and specific.

Consider the special case of the identity where a is 1:
1-x² = (1-x)(1+x)

There is a nice financial interpretation of this. If an item has a 10% sales tax (corresponding to x=0.1), and has a 10% discount, then the final price is not the same as the initial price, but is instead reduced by 1% (since x²=0.1²=0.01 ie 1%). Also, since (1-x)(1+x) and (1+x)(1-x) are the same, it doesn't matter whether the discount is done first or last.

Two Formulas for Hyperbolas

When I first learned about the hyperbola, back in high school, it was via the equation y = 1/x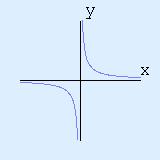

The instructor told us that the curve was called the hyperbola, and went on to talk about asymptotic behaviour, the two asymptotes (x=0 and y=0) and all the usual things. No problem! We then moved on to other topics.

A few weeks later, we tackled second order equations in the plane: ie Ax² + By² + Cxy + Ex + Dy + F = 0. We then got to the equation x²-y²=1, and we were told that it was a hyperbola, and the two asymptotes were x=y and x=-y.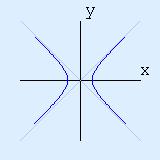

It seems I was the only one who noticed and was disturbed by the fact that a "hyperbola" had been defined twice, and in two different ways that seemed unrelated. The instructor didn't talk about this. Our textbook, which was geared towards preparing for an exam, had nothing to say on the topic. I somehow convinced myself that the equations were defining the same kind of curve. I forget just how I did it, but I certainly didn't "understand". I probably manipulated some symbols, and magically everything worked out. It was years later that I finally realized that the two equations were easily reconciled via the a²-b²=(a-b)(a+b) identity. It's a little more obvious if y=1/x is rewritten as xy=1. Somehow, I don't think that would have been enough of a clue for me when I was in high school. Some things take time.

Just to say a little more about this, we have that the co-ordinate transform
u=x-y
v=x+y
changes the equation uv=1 to (x-y)(x+y)=1, which is x²-y²=1.

The transform described here is a 45° rotation followed by a scaling (with the scaling factor being √2). If we stick to rotations, the transformation to consider is
u=(x-y)/√2
v=(x+y)/√2
uv=1 now becomes x²-y²=2, not x²-y²=1. If you had looked carefully at the above diagrams, you might have noticed that the x²-y²=1 hyperbola approached its asymptotes faster than the xy=1 hyperbola. Now you know why.

Wave Equation

A solution U(x,t) to the one dimensional wave equation in two variables x and t is a solution to the partial differential equation:
d²U/dx - d²U/dt = 0
which, in differential operator form, is just
[ (d/dx)² - (d/dt)² ] U = 0

As we saw earlier, the a²-b² identity applies as long as ab=ba. In the case where a and b are the differential operators d/dx and d/dt, we have that ab=ba, ie (d/dx)(d/dt) = (d/dt)(d/dx) since d²f/dxdt = d²f/dtdx. So, the wave equation becomes (d/dx - d/dt) (d/dx + d/dt) U = 0

Writing
x = u+v
t = u-v
we have
d/du = (dx/du)(d/dx) + (dt/du)(d/dt) = (d/dx)+(d/dt)
d/dv = (dx/dv)(d/dx) + (dt/dv)(d/dt) = (d/dx)-(d/dt)
These are precisely the terms in the factorization of (d/dx)² - (d/dt)² and so the wave equation becomes (d/dv)(d/du)U=0

The solution to this is "trivial": U = f(u) + g(v) = f((x+t)/2) + g((x-t)/2), i.e.
U(x,t) = F(x+t) + G(x-t)

The factorization given by the a²-b² identity ends up telling us that any solution to the wave equation is the superposition of a wave moving to the left at speed 1, and a wave moving to the right at speed 1.

Inner Products and Length Squared

For two vectors u=(u₁,u₂,u₃) and v=(v₁,v₂,v₃), the inner product u•v is given by
u₁v₁+u₂v₂+u₃v₃

For a vector v=(v₁,v₂,v₃), the length squared |v|² is
v₁v₁+v₂v₂+v₃v₃

It's pretty clear that they're related:
|v|² = v•v
ie, the length squared function s(v)=|v|² is derivable from the inner product function p(u,v) = u•v, via
s(v)=p(v,v)

The a²-b² identity applies in this situation, where multiplication is the dot product, and squaring is length squared:

|u|²-|v|² = (u-v)•(u+v)

This is mildly interesting, but the equivalent form of the identity, which relates a product to a difference of squares is really interesting:

u•v = |(u+v)/2|²-|(u-v)/2|²

This tells us that the inner product function is derivable from the length squared function:
p(u,v)=s((u+v)/2)-s((u-v)/2)

And, of course, there's nothing special about R³ with the standard inner product. Everything generalizes to semidefinite products and to Hilbert spaces.

Patterns in the Multiplication Table

When I was in elementary school, we memorized our multiplication table all the way up to the 12 by 12 case. We were tested over and over, year after year. We got to know that multiplication table!

*	1	2	3	4	5	6	7	8	9	10	11	12
1	1	2	3	4	5	6	7	8	9	10	11	12
2	2	4	6	8	10	12	14	16	18	20	22	24
3	3	6	9	12	15	18	21	24	27	30	33	36
4	4	8	12	16	20	24	28	32	36	40	44	48
5	5	10	15	20	25	30	35	40	45	50	55	60
6	6	12	18	24	30	36	42	48	54	60	66	72
7	7	14	21	28	35	42	49	56	63	70	77	84
8	8	16	24	32	40	48	56	64	72	80	88	96
9	9	18	27	36	45	54	63	72	81	90	99	108
10	10	20	30	40	50	60	70	80	90	100	110	120
11	11	22	33	44	55	66	77	88	99	110	121	132
12	12	24	36	48	60	72	84	96	108	120	132	144

In high school, my good friend Jack Robin told me that he'd discovered a pattern in the multiplication table, and he started describing it to me. If you moved off the main diagonal, consisting of squares, via the other diagonal direction, the values went down by one. At first I didn't understand what he was talking about, but he showed it to me, and he was right. I'd never noticed that before.

*	1	2	3	4	5	6	7	8	9	10	11	12
1	1	2	3	4	5	6	7	8	9	10	11	12
2	2	4	6	8	10	12	14	16	18	20	22	24
3	3	6	9	12	15	18	21	24	27	30	33	36
4	4	8	12	16	20	24	28	32	36	40	44	48
5	5	10	15	20	25	30	35	40	45	50	55	60
6	6	12	18	24	30	36	42	48	54	60	66	72
7	7	14	21	28	35	42	49	56	63	70	77	84
8	8	16	24	32	40	48	56	64	72	80	88	96
9	9	18	27	36	45	54	63	72	81	90	99	108
10	10	20	30	40	50	60	70	80	90	100	110	120
11	11	22	33	44	55	66	77	88	99	110	121	132
12	12	24	36	48	60	72	84	96	108	120	132	144

The next question was: why? As it turned out, we'd just been learning algebra, and I was able to make the connection! It was just an application of the a²-b² identity:
(n-1)(n+1) = n²-1

Sums of Consecutive Odd Numbers

One of the special cases of the identity is:
x²-(x-1)² = 2x-1

After years of having my mind deformed by programming, it seems really natural to start at a positive integer n, and iterate down to 1. Doing that, we get:

n2	-	(n-1)2	=	2n-1
(n-1)2	-	(n-2)2	=	2n-3
(n-2)2	-	(n-3)2	=	2n-5
		…
32	-	22	=	5
22	-	12	=	3
12	-	02	=	1

Adding up the columns, we get
n² = 1+3+…+(2n-3)+(2n-1)

It's also true that if we hadn't gone all the way to one, but only went down to m+1, we would get:
n² = m² + (2m+1) + (2m+3) + … + (2n-1)

Cracking RSA

RSA encryption (named after Rivest Shamir and Adleman) wouldn't provide much protection if we knew how to factor large numbers quickly. In particular, given two large primes p and q, if we could factorize the product, N=pq quickly, RSA encryption would be broken.

The a²-b² identity gives us a way of factorizing quickly, if p and q aren't chosen properly.

Before going into details, I'd like to digress a little and say a little bit more about RSA encryption.

If you study the subject, something that you'll quickly learn is that what we really want to get is φ(N), where φ is Euler's phi function. Since φ(N)=(p-1)(q-1), factorizing N will certainly allow you to get φ(N). It's also true that knowing φ(N) will allow you to get the factorization. This is because knowing N=pq and φ(N)=(p-1)(q-1) will give you p+q, via N+1-φ(N). Well, once you have pq and p+q, the identity gives us p-q via pq = ((p+q)/2)² - ((p-q)/2)². And, once we have both p+q and p-q we have p and q.

Okay, that's the end of the digression.

Although factorizing N=pq is hard in general, if p and q are chosen badly, then the factorization is easy. The obvious case, that takes little mathematical sophistication to realize, is that if p is small, say smaller that 10¹⁰, then simply testing p=2, then p=3, then p=4, etc, will quickly give the game away. Gigahertz machines can check a mere 10¹⁰ cases pretty quickly. So, don't pick p and q to be to close to the extremes. i.e. if pq is a 200 digit number, don't pick p and q so that p has a mere 10 digits, and q has 190 digits.

As it turns out, you don't want to be too close to the middle either, by which I mean don't pick p and q so that p has 100 digits, q has 100 digits, and p and q differ only in the least significant 55 digits. The reason is because of the identity!

Suppose K² is a perfect square greater that N. If K²-N is a perfect square J², then N=K²-J² instantly gives us the factorization (K-J)(K+J).

So, instead of iterating p starting from 2 and counting up, we can start from M=K²-N, where K² is the smallest square greater than N, and increment by 2K+1, then 2K+3, then 2K+5 etc to get M=(K+1)²-N, M=(K+2)²-N, M=(K+3)²-N, and at each stage test to see if M is a square. In the 200 digit example above, it would take a mere 10¹⁰ steps to find p and q.

By the way, currently there isn't any well-known proof establishing that factorizing N=pq is difficult in general.

Recursion and Continued Fractions

There's a recursive formula hiding in the identity, and it leads to continued fraction expressions. Here are the details:

The identity can be written as
x-y = (x²-y²)/(x+y)

This can be viewed as a way of writing x-y in terms of x+y. But x+y can be written in terms of x-y via simple addition, ie x+y=2y+(x-y).

So, we have a formula for x+y in terms of x+y! Here it is:
x+y = 2y + (x²-y²)/(x+y)

Well, once we have something like that, it's hard to resist recursing infinitely to get:
x+y = 2y + (x²-y²)/ ( 2y + (x²-y²)/ ( 2y + (x²-y²)/ … ) )

Choosing x and y so that x²-y² is something simple, like 1, we get that x must be √(1+y²). Using this, the formula becomes: y+√(1+y²) = 2y + 1/(2y+1/(2y+1/…)). In the well known continued fraction notation. This is saying y+√(1+y²) = [2y,2y,2y,…]

Some immediate consequences are:

for y=1/2, we get that φ, the golden ratio (1+√5)/2 satisfies φ = [1,1,1,…] leading to approximations via ratios of Fibonacci numbers
1/1, 2/1, 3/2, 5/3, ….

Writing y=n, we get that
n + √(1+n²) = [2n, 2n, 2n, …]
This tells us that
√(n²+1) = [n, 2n, 2n, …]

For example, taking n=1, we get that
√2 = [1, 2, 2, …]
leading to the approximations 1/1, 2/1, 3/2, 7/5, 17/12, …

Recursion and an Infinite Product

There's another recursive formula hiding in the identity, and it leads to an infinite product, which in turn leads to an infinite series. Here are the details:

Consider the special case
1-x²= (1-x)(1+x)
This can be viewed as a formula for 1/(1-x), namely
1/(1-x) = (1+x)/(1-x²)

Well, viewing x² as a single variable u, this is saying
1/(1-x) = (1+x) (1/(1-u))

Now apply the 1/(1-x) formula to 1/(1-u), and we're well on our way to infinite recursion:
1/(1-x) = (1+x)(1+u)(1/(1-u²))

This process leads to the infinite product
1/(1-x) = (1+x)(1+x²)(1+x⁴)(1+x⁸)…

Multiplying out, this gives the well-known series 1/(1-x) = 1 + x +x² + x³ + x⁴ + …

Feedback

If you have corrections, additions, modifications, etc please let me know mailto:walterv@gbbservices.com