Views of the Hopf Fibration

Introduction

Here are some animated anaglyphs that make use of the Hopf fibration. These anaglyphs are inspired by Frank Farris' animated gif, which is shown below:

When I first saw this animated gif, I was very impressed. The use of colors and animation helps greatly in appreciating the three dimensional nature of the fibration. Having done my share of 3d graphics programming, and being a big fan of anaglyphs, it occurred to me that it might be interesting to create some animated anaglyphs that do something similar.

Frank Farris kindly supplied me with the maple worksheet he used to generate his images. I translated that to python code, used the PIL (python imaging library) to do the imaging, and generated all the images below. I hope you enjoy them.

Looking down the z axis

To see the anaglyphs, you'll need to wear glasses for which the left lens is red, and the right lens is blue, green or cyan.

The following anaglyph should require a minimal amount of eye adjustment. The region you're looking at should be partly in front of the monitor, and partly behind the monitor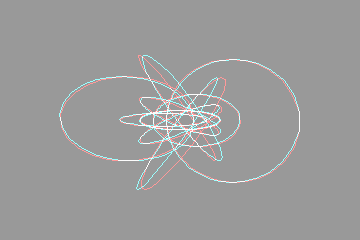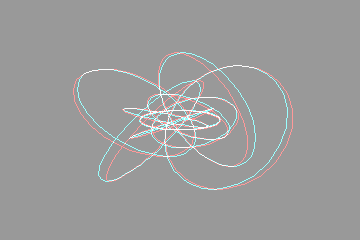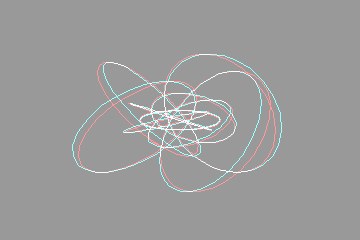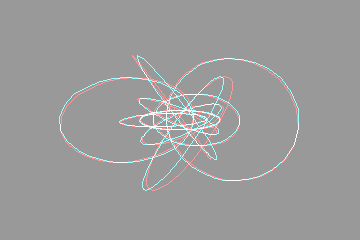

Here's a side by side comparison of the two animated gifs.

The next anaglyph will require more eye adjustment. The entire region under consideration should appear to hover in mid air, a few inches in front of the monitor. Too see it, you will have to focus on a point roughly three inches in front of the monitor

I like to orient myself with the x,y,z axes. They're included below: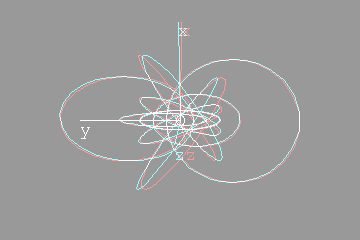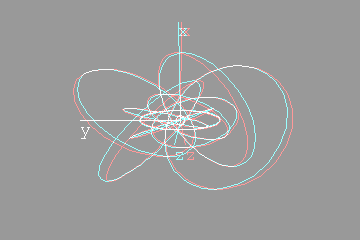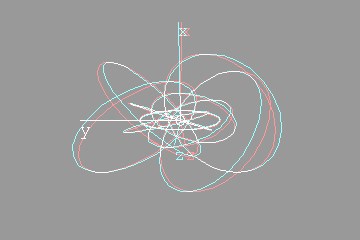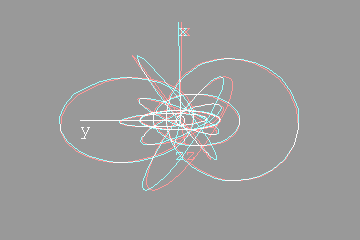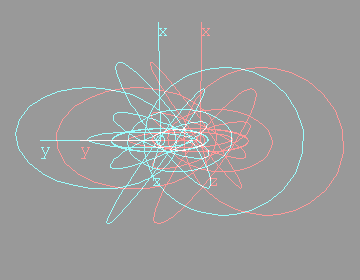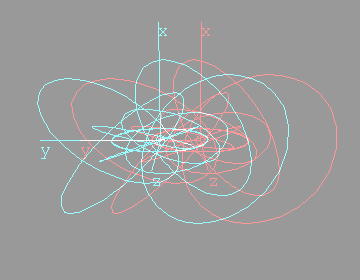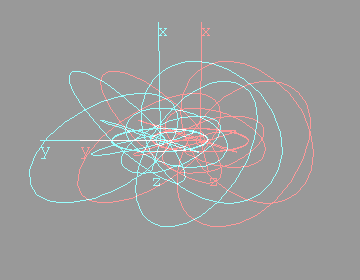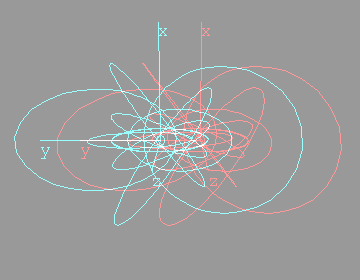

Looking down the x axis

Here's the same sequence of four anaglyphs, except that we're looking down the x-axis.

Without axes:

Hovering in space: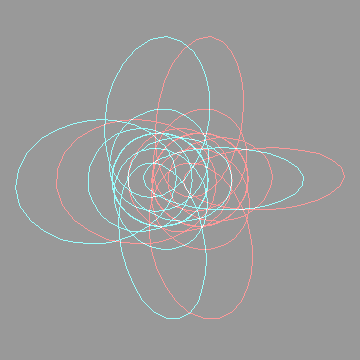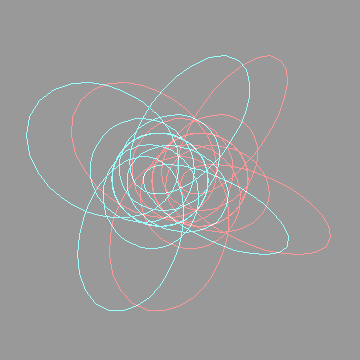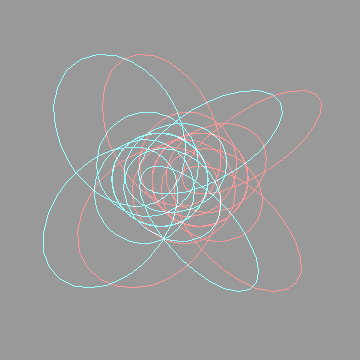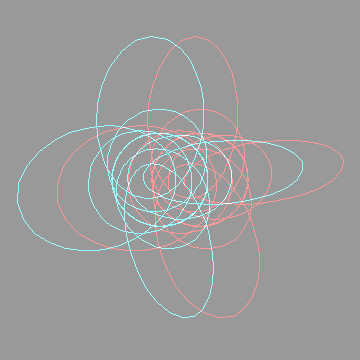

With axes:

Hovering in space:

Feedback

If you have corrections, additions, modifications, etc please let me know mailto:walterv@gbbservices.com